Chapter 3 – Understanding Quadrilaterals
Key Notes
A simple closed curve made up of only line segments is called a polygon.
A diagonal of a polygon is a line segment connecting two nonconsecutive vertices.
A convex polygon is a polygon in which no portion of its any diagonal is in its exterior.
A concave polygon is a polygon in which at least one portion of its any diagonal is in its exterior.

A quadrilateral is a polygon having only four sides.
A regular polygon is a polygon whose all sides are equal and also all angles are equal.
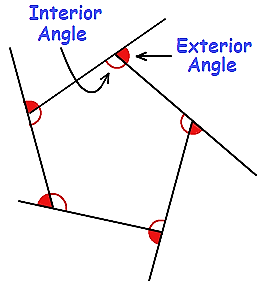
Interior and Exterior angles
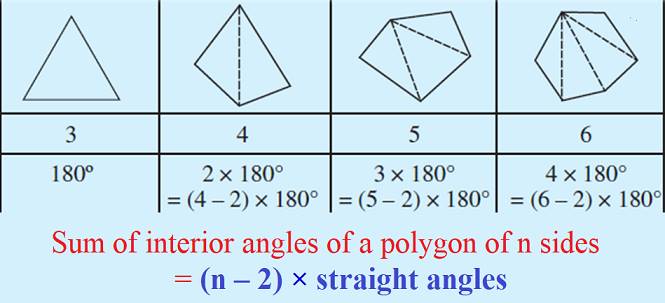
The sum of interior angles of a polygon of n sides is (n – 2) × straight angles.
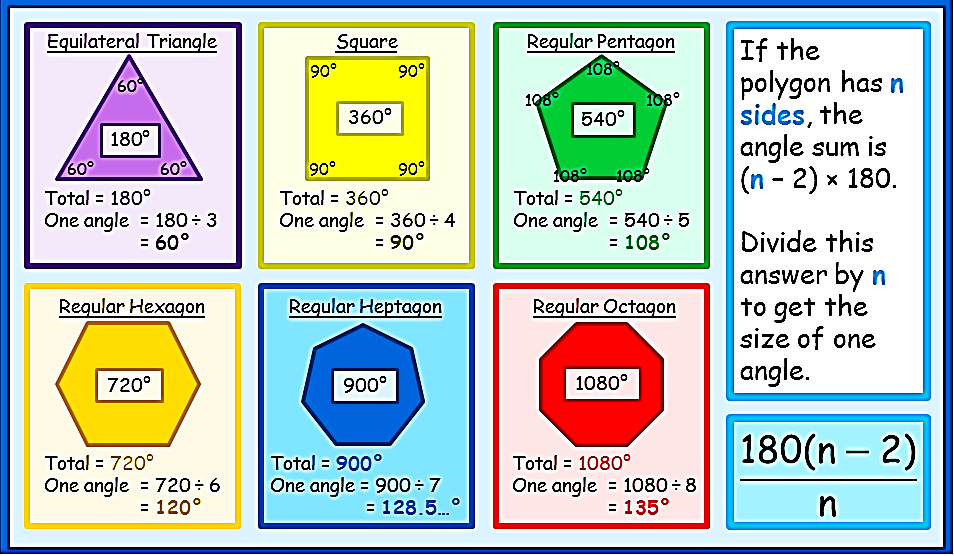
Each interior
angle of a regular polygon = ![]()
Angle Sum Property: The sum of interior angles of a quadrilateral is 360°.
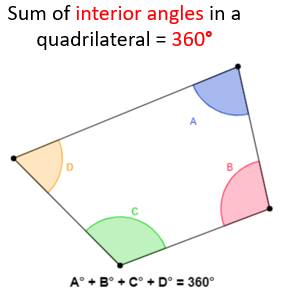
Note: Above property is applicable for quadrilateral only
The sum of exterior angles, taken in an order, of a polygon is 360°.
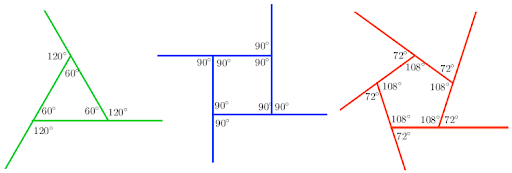
![]()
Trapezium is a quadrilateral in which a pair of opposite sides is parallel.

Kite is a quadrilateral which has two pairs of equal consecutive sides.
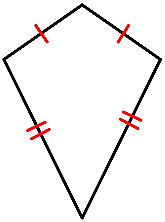
A parallelogram is a quadrilateral in which each pair of opposite sides is parallel.
A rhombus is a parallelogram in which adjacent sides are equal.
In a rhombus diagonals intersect at right angles.
A rectangle is a parallelogram in which one angle is of 90°.
In a rectangle diagonals are equal.
A square is a parallelogram in which adjacent sides are equal and one angle is of 90°.
In a parallelogram, opposite sides are equal, opposite angles are equal and diagonals bisect each other.
Number of diagonals in a polygon of n sides = ![]()
A quadrilateral can be constructed uniquely if
• the lengths of its four sides and a diagonal are given.
• the lengths of its three sides and two diagonals are given.
• its two adjacent sides and three angles are given.
• its three sides and two included angles are given.
Online Tuitions & Self-Study Courses for Grade 6 to 12 & JEE / NEET
