Decimals

The numbers used to represent numbers smaller than unit 1 are called decimal numbers.

Decimals are used to show the part of a whole number.

A decimal point or period separates the fractional part and whole number part in a decimal number.

0.7

Place value of a digit can be defined as the value of a digit as per the place of that digit in a number.

Tenths

As we know that 1 cm = 10 mm, so if we have to find the opposite then

1 mm = 1/10 cm or one-tenth cm or 0.1 cm.

Hence, the first number after the decimal represents the tenth part of the whole.

This reads as “thirty-four point seven”.

A more exhaustive representation of decimal numbers is given below.

Let us find different place values of each digit in the decimal number 0.7654.

The value of the digit at the first place after the decimal point is tenths place value. Tenths can be calculated as 1 unit divided in 10 equal parts i.e., 0.1. Therefore, considering this there are 7 tenths in the number 0.7654.

The value of the digit at the second place after the decimal point is hundredths place value. The number in that place tells you how many hundredths are there. Hundredths can be calculated as 1 unit divided in100 equal parts i.e., 0.01. Therefore, considering this there are 6 hundredths in the number 0.7654.

The value of the digit at the third place after the decimal point is thousandths place value. The number in that place tells you how many thousandths are present. Thousandths can be calculated as 1 unit divided in1000 equal parts i.e., 0.001. Therefore, considering this there are 5 thousandths in the number 0.7654.

The value of the digit at the fourth place after the decimal point is ten-thousandths place value. The number in that place tells you how many ten-thousandths are present. Ten-thousandths can be calculated as 1 unit divided into 10000 equal parts i.e., 0.0001. Therefore, considering this there are 4 thousandths in the number 0.7654.

Example: Consider the number 95.487016. For each of the following digits, give its place value:

(a) 6

(b) 7

(c) 8

(d) 9

(e) 0

Solution:

(a) 6 = millionths

(b) 7 = thousandths

(c) 8 = hundredths

(d) 9 = tens

(e) 0 = ten thousandths

Representation of Decimals on Number Line

To represent decimals on the number line we have to divide the gap of each number into 10 equal parts as the decimal shows the tenth part of the number.

Example:

Show 0.3, 0.8, 1.5, 2.4, 3.7 and 4.6 on the number line.

Solution:

All the numbers are greater than 0 and less than 5. Hence, we have to make a number line with 0 and 5 at ends and divide it in 5 equal parts. Then, we need to divide each part in 10 equal parts.

Then mark as shown below.

Fractions as Decimals

It is easy to write the fractions with 10 as the denominator in decimal form but if the denominator is not 10 then we have to find the equivalent fraction with denominator 10.

Example:

Convert 12/5 and 3/2 in decimal form.

Solution:

Decimals as Fractions

Example:

Write 2.5 in a fraction.

Solution:

Example:

If 25 out of 100 squares are shaded then how will you write it in fraction and decimal form?

Solution:

25 is a part of 100, so the fraction will be 25/100.

In the decimal form we will write it as 0.25.

Place Value Chart

This is the place value chart which tells the place value of each digit in the decimal number. It makes it easy to write numbers in decimal form.

Example:

With the given place value chart write following number in the decimal form.

Hundreds (100)	Tens (10)	Ones (1)	Tenths (1/10)	Hundredths (1/100)
4	6	3	8	5

Solution:

According to the above table-

Comparing Decimals

1. If the whole number is different.

If the whole numbers of the decimals are different then we can easily compare them. The number with the greater whole number will be greater than the other.

Example:

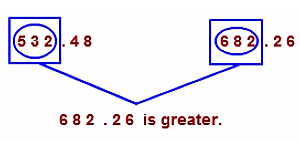
Compare 532.48 and 682.26.

Solution:

As the whole numbers are different, so we can easily find that the number with a greater whole number is greater.

Hence 682.26 > 532.48

2. If the whole number is the same

If the whole numbers of the decimals are same then we will compare the tenth and then the hundredth part if required.

The number with the greater tenth number is greater than the other.

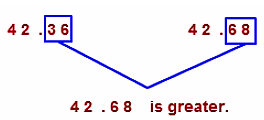
Example:

Compare 42.36 and 42.68.

Solution:

As the whole number is the same in both the numbers so we have to compare the tenth part.

Hence 42.68 > 42.36

Example:

Write 25 paise in decimals.

Solution:

100 paise = 1 Rs.

1 paise = 1/100 Rs. = 0.01 Rs.

25 paise = 25/100 Rs. = 0.25 Rs.

Example:

Write 7 rupees and 35 paise in decimals.

Solution:

7 rupees is the whole number, so

7 + 35/100 = 7 + 0.35 = 7.35 Rs.

Example:

If the height of Jamie is 175 cm then what will be his height in meters?

Solution:

100 cm = 1 m

1 cm = 1/100 m = 0.01 m

175 cm = 175/100 m

Hence, the height of Jamie is 1.75 m.

Example:

If the weight of David’s school bag is 4725 grams then what will be its weight in a kilogram?

Solution:

1000 gm = 1 kg

1 gm = 1/1000 kg = 0.001 kg

Addition of Decimal numbers

To add the decimal numbers, we can add them as whole numbers but the decimal will remain at the same place as it was in the given numbers. It means that we have to line up the decimal point in each number while writing them, and then add them as a whole number.

Example:

Add 22.3 and 34.1

Solution:

First we line up the numbers, i.e., place them in such a way that decimals are one over the other, and then add them.

Example:

Add 1.234 and 4.1.

Solution:

There are three numbers after decimal in one number and one number after decimal in another number. We write the numbers by lining up the decimal points of both the numbers, then add them.

Another way is to write the numbers in the place value chart, so that it will be easy to identify, how to write numbers.

	Ones (1)	Tenths (1/10)	Hundredths (1/100)	Thousandths (1/1000)
	1	2	3	4
+	4	1	0	0
=	5	3	3	4

Subtraction of Decimal Numbers

Subtraction is also done as normal whole numbers after lining up the decimals of the given number.

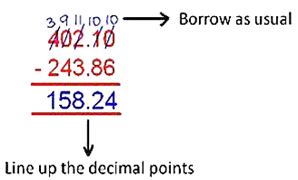
Example:

Subtract 243.86 from 402.10.

Solution:

¨     Write the numbers in a line so that the decimal points of both the numbers lined up.

¨     Then subtract and borrow as we do in whole numbers.

¨     Line up the decimal point in the answer also.

  

Example:

Subtract 27.59 from 31.40.

Solution:

¨     Write the numbers in a line so that the decimal points of both the numbers lined up.

¨     Then subtract and borrow as we do in whole numbers.

¨     Line up the decimal point in the answer also.

 

Example:

Subtract 79.79 from 89.

Solution:

¨     Convert both decimals in like terms (having same number of decimal places), i.e., write 89 as 89.00

¨     Write the numbers in a line so that the decimal points of both the numbers lined up.

¨     Then subtract and borrow as we do in whole numbers.

¨     Line up the decimal point in the answer also.