Class 11 Chemistry

Chapter 2 – Structure of Atom

Study Notes

Atom is the smallest particle which exhibits all the properties of its matter. It may or may not have self-existence. Atom is made of subatomic particles like electron, proton and neutrons.

The neutron and proton have approximately equal masses of 1 u and the electron is about 1837 times lighter, its mass can sometimes be neglected as an approximation.

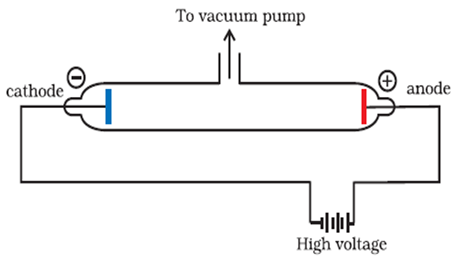
Electrons were discovered using cathode ray discharge tube experiment.

Nucleus was discovered by Rutherford in 1911.

Cathode ray discharge tube experiment:

A cathode ray discharge tube made of glass is taken with two electrodes. At very low pressure (0.01 mm of Hg) and high voltage (approx 10000 volts), current starts flowing through a stream of particles moving in the tube from cathode to anode. These rays were called cathode rays. When a perforated anode was taken, the cathode rays struck the other end of the glass tube at the fluorescent coating and a bright spot on the coating was developed.

Results:

a. Cathode rays consist of negatively charged electrons.

b. Cathode rays themselves are not visible but their behaviour can be observed with help of fluorescent or phosphorescent materials.

c. In absence of electrical or magnetic field cathode rays travel in straight lines

d. In presence of electrical or magnetic field, behaviour of cathode rays is similar to that shown by electrons

e. The characteristics of the cathode rays do not depend upon the material of the electrodes and the nature of the gas present in the cathode ray tube.

Charge to mass ratio of an electron (cathode rays) was determined by Thomson. The charge to mass ratio of an electron is

 1.758820 × 10¹¹ C kg^–1 = 1.758820 × 10⁸ C g^–1

Charge on an electron was determined by R. A. Millikan by using an oil drop experiment. The value of the charge on an electron is –1.6 × 10^–19 C.

The mass on an electron was determined by combining the results of Thomson’s experiment and Millikan’s oil drop experiment. The mass of an electron was determined to be 9.1094 × 10^–31 kg.

Discovery of protons: Modified cathode ray tube experiment was carried out which led to the discovery of protons.

Canal rays (Anode rays) are simply the positively charged gaseous ions. The smallest and lightest positive ion was obtained from hydrogen and was called proton.

Neutrons were discovered by James Chadwick by bombarding a thin sheet of beryllium by α-particles (He²⁺). They are electrically neutral particles having a mass slightly greater than that of the protons.

Atomic number (Z) : The number of protons present in the nucleus (Moseley 1913). It is equal to the number of electrons in a neutral atom.

Mass Number (A): Sum of the number of protons and neutrons present in the nucleus.

Atomic number (Z) = No. of protons = No. of e^- in neutral atom

Mass number (A) = No. of protons + No. of neutrons

A = P + N

A = Z + N

A = e^- + N (in neutral atom)

Radius of nucleus of an atom

Where  = 1.4 × 10^–15 m (Constant)

In a negative ion, X^n–, No. of electrons = Z + n

In a Positive ion, Mⁿ⁺, No. of electrons = Z – n

However, no. of protons and neutrons do not change.

Thomson model of an atom:

a.    An atom possesses a spherical shape in which the positive charge is uniformly distributed.

b.   Known as plum pudding, raisin pudding or watermelon model

c.    Feature: The mass of an atom is assumed to be uniformly distributed across the atom.

Rutherford’s model of an atom:

a.    A stream of high-energy α-particles from a radioactive source was directed at the thin gold foil.

b.   Gold foil had a circular fluorescent screen (of zinc sulphide) around it.

c.    A tiny flash of light was observed at the point, whenever an α-particle struck the screen.

This model explained that atom consists of nucleus which is concentrated in a very small volume. The nucleus comprises of protons and neutrons. The electrons revolve around the nucleus in fixed orbits. Electrons and nucleus are held together by electrostatic forces of attraction.

Observations from α- particles scattering experiment by Rutherford:

a. Most of the α- particles passed through gold foil undeflected

b. A small fraction of α- particles got deflected through small angles

c. Very few α- particles did not pass through foil but suffered large deflection nearly 180^o.

Conclusions Rutherford drew from α- particles scattering experiment:

a. Since most of the α-particles passed through foil undeflected, it means most of the space in atom is empty

b. Since some of the α-particles are deflected to certain angles, it means that there is some positive mass present in atom

c. Since only some of the α-particles suffered large deflections, the positively charged mass must be occupying very small space

d. Strong deflections or bouncing back of α-particles from metal foil were due to direct collision with positively charged mass in atom

Drawbacks of Rutherford’s model of atom:

a. According to Rutherford’s model of atom, electrons which are negatively charged particles revolve around the nucleus in fixed orbits. When a body is moving in an orbit, it undergoes acceleration (even if the body is moving with a constant speed in an orbit, it must accelerate because of changing direction). According to electromagnetic theory of Maxwell, a charged particle undergoing acceleration should emit electromagnetic radiation. Thus, an electron in an orbit should emit radiation. Thus, the orbit should shrink. But this does not happen.

Thus, the Rutherford model cannot explain the stability of an atom.

b. The model does not give any information about how electrons are distributed around nucleus and what are energies of these electrons.

Isotopes: These are the atoms of the same element having the same atomic number but different mass number. E. g., , ,

Isobars: Isobars are the atoms of different elements having the same mass number but different atomic number. e g  and

Isotones: Atoms of different elements having same number of neutrons. E.g.  ,  

Isoelectronic species: These are those species which have the same number of electrons.

Nuclear isomers: Atoms with the same atomic and mass numbers but different radioactive properties, e.g., uranium X (half-life 1.4 min) and uranium Z (half-life 6.7 hours).

Atomic mass unit: Exactly equal to 1/12^th of the mass of one  atom.

a.m.u.: 1 a.m.u. = 1.66 × 10^-24 g

Electromagnetic radiations:

The radiations which are associated with electrical and magnetic fields are called electromagnetic radiations. When an electrically charged particle moves under acceleration, alternating electrical and magnetic fields are produced and transmitted. These fields are transmitted in the form of waves. These waves are called electromagnetic waves or electromagnetic radiations.

Properties of electromagnetic radiations:

a. Oscillating electric and magnetic field are produced by oscillating charged particles. These fields are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.

b. They do not need a medium to travel. That means they can even travel in vacuum.

There are many types of electromagnetic waves which differ from one another in wavelength (or frequency). These electromagnetic radiations constitute electromagnetic spectrum.

Characteristics of electromagnetic radiations:

a. Wavelength (λ): It may be defined as the distance between two neighbouring crests or troughs of wave as shown. It is denoted by λ.

b. Frequency (ν): It may be defined as the number of waves which pass through a particular point in one second.

c. Velocity (v): It is defined as the distance travelled by a wave in one second. In vacuum all types of electromagnetic radiations travel with the same velocity. Its value is 3.0 × 10⁸ m sec^–1. It is denoted by c.

Velocity = frequency × wavelength

c = νλ

d. Wave number (): Wave number is defined as the number of wavelengths per unit length.

Wave nature of electromagnetic radiation failed to explain many phenomena such as black body radiation and photoelectric effect.

Black Body Radiation

o   Solids on heating emit radiations over a wide range of wavelengths.

o   Radiations emitted shift from lower frequency to a higher frequency as the temperature increases.

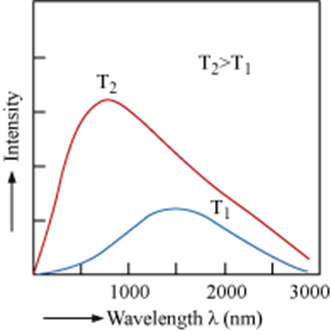
o   An ideal body which absorbs and emits all radiation is called a black body and the radiation emitted by it is called black body radiation.

o   An ideal black body is defined as a perfect absorber and a perfect emitter of radiations.

o   The distribution of frequency of the emitted radiation from a black body depends upon temperature.

o   The intensity of emitted radiation at a given temperature increases with the decrease in wavelength. It attains a maximum value at a given wavelength and then starts decreasing with further decrease of wavelength.

These experimental results cannot be explained on the basis of wave theory of light.

Photoelectric Effect

o   When certain metals such as potassium, rubidium, cesium, etc. are exposed to a beam light, the electrons are ejected from the surface of the metals as shown in the figure.

o   The phenomenon is called Photoelectric effect.

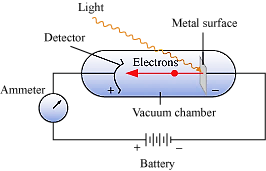
Results of the Experiment

o   The electrons are ejected from the surface of the metal as soon as the beam strikes the metal surface.

o   The number of electrons ejected from the metal surface is directly proportional to the intensity of light.

o   For each metal, there is a certain minimum frequency of light below which photoelectric effect is not observed. This minimum frequency is called threshold frequency ().

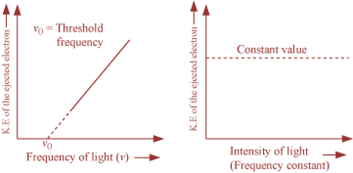
o    When , the ejected electrons come out with certain kinetic energy. The kinetic energy of the emitted electrons is directly proportional to the frequency of incident radiation and is independent of incident radiation.

The results of photoelectric effect could not be explained by using law of classical physics.

Planck's Quantum Theory: (Particle Nature of Electromagnetic Radiation)

o  The radiant energy is emitted or absorbed not continuously but discontinuously in the form of small discrete packets of energy called ‘quantum’. In case of light, the quantum of energy is called a ‘photon’.

o The energy of each quantum is directly proportional to the frequency of the radiation, i.e. E ∝ υ or E = hυ where h = Planck’s constant = 6.626 × 10^–27 Js

o Energy is always emitted or absorbed as integral multiple of this quantum. E = nhυ where n = 1,2,3,4,.....

Explanation of Photoelectric Effect Using Quantum Theory

According to Einstein,

Energy of the striking photon = Binding energy + Kinetic energy of ejected electron

If ν < ν₀, then no electrons will be ejected, no matter how high the intensity is.

If ν > ν₀, then the excess energy is imported to the ejected electron as kinetic energy. As the frequency of radiation increases, the kinetic energy of the electron will increase.

As the intensity increases, more electrons will be ejected, but their kinetic energy does not change.

Dual Behaviour of Electromagnetic Radiations

Some phenomena (reflection, refraction, diffraction) were explained using wave nature of electromagnetic radiation and some phenomena (photoelectric effect and black body radiation) were explained by using particle nature of radiation.

This suggests that microscopic particles exhibit wave-particle duality.

The Bohr's Atomic Model

Bohr's main postulates can be summarised as

(i) The single electron goes around the nucleus in a circular orbit.

(ii) The energy of an electron in the orbit does not change with time. Electron will move from a lower stationary state to a higher stationary state when required amount of energy is absorbed by the electron or energy is emitted when electron moves from higher stationary state to lower stationary state.

(iii) The frequency of radiation absorbed or emitted when transition occurs between two stationary states that differ in energy by ΔE, is given by:

(iv) The circulating electron can have only those angular momentum values which are integral multiples of h/2π.

According to Bohr’s theory for hydrogen atom:

a) The stationary states for electron are numbered n = 1,2,3.......... These integral numbers are known as Principal quantum numbers.

b) The radii of the stationary states are expressed as:

r_n = n² a₀

where a₀ = 52.9 pm. Thus, the radius of the first stationary state, called the Bohr radius, is 52.9 pm. Normally the electron in the hydrogen atom is found in this orbit (that is n = 1). As n increases the value of r will increase. In other words, the electron will be present away from the nucleus.

c) The most important property associated with the electron, is the energy of its stationary state. It is given by the expression.

where R_H is called Rydberg constant and its value is 2.18×10^–18 J.

d) Bohr’s theory can also be applied to the ions containing only one electron, similar to that present in hydrogen atom. For example, He⁺, Li²⁺, Be³⁺ and so on.

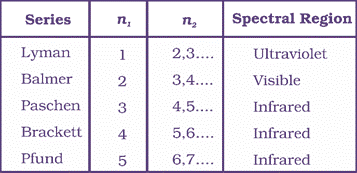
Line Spectrum of Hydrogen atom

The hydrogen spectrum consists of several series of lines named after their discoverers.

The Swedish spectroscopist, Johannes Rydberg, noted that all series of lines in the hydrogen spectrum could be described by the following expression:

 

where n₁ = 1, 2 ........

     n₂ = n₁ + 1, n₁ + 2 ......

The value 109677 cm^–1 is called the Rydberg constant for hydrogen.

The first five series of lines that correspond to n1 = 1, 2, 3, 4, 5 are known as Lyman, Balmer, Paschen, Bracket and Pfund series, respectively.

Shortcomings of Bohr’s theory:

(i) It fails to account for the finer details (doublet, that is two closely spaced lines) of the hydrogen atom spectrum observed by using sophisticated spectroscopic techniques.

(ii) This model is also unable to explain the spectrum of atoms other than hydrogen, for example, helium atom which possesses only two electrons.

(iii) Further, Bohr’s theory was also unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect).

(ii) It could not explain the ability of atoms to form molecules by chemical bonds. In other words, taking into account the points mentioned above, one needs a better theory which can explain the salient features of the structure of complex atoms.

Dual Behaviour of Matter

The French physicist, de Broglie in 1924 proposed that matter, like radiation, should also exhibit dual behaviour i.e., both particle and wavelike properties. This means that just as the photon has momentum as well as wavelength, electrons should also have momentum as well as wavelength, de Broglie, from this analogy, gave the following relation between wavelength (l) and momentum (p) of a material particle.

 

where m is the mass of the particle, v its velocity and p its momentum.

Heisenberg’s Uncertainty Principle

Werner Heisenberg a German physicist in 1927, stated uncertainty principle which is the consequence of dual behaviour of matter and radiation. It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron.

Mathematically, it can be given as in equation

 

or   

or   

where ∆x is the uncertainty in position and ∆p (or ∆v) is the uncertainty in momentum (or velocity) of the particle.

The effect of Heisenberg Uncertainty Principle is significant only for motion of microscopic objects and is negligible for that of macroscopic objects.

Reasons for the Failure of the Bohr Model

One can now understand the reasons for the failure of the Bohr model. In Bohr model, an electron is regarded as a charged particle moving in well-defined circular orbits about the nucleus. The wave character of the electron is not considered in Bohr model.

Further, an orbit is a clearly defined path and this path can completely be defined only if both the position and the velocity of the electron are known exactly at the same time. This is not possible according to the Heisenberg uncertainty principle.

Quantum Mechanical Model of Atom

Erwin Schrödinger, in 1926, proposed an equation called Schrödinger equation of quantum mechanics to describe the electron distributions in space and the allowed energy levels in atoms. This equation incorporates de Broglie’s concept of wave-particle duality and is consistent with Heisenberg uncertainty principle.

 This equation is quite complex and knowledge of higher mathematics is needed to solve it. You will learn its solutions for different systems in higher classes.

For a system (such as an atom or a molecule whose energy does not change with time) the Schrödinger equation is written as Hψ = Eψ where H is a mathematical operator called Hamiltonian.

When Schrödinger equation is solved for the electron in a hydrogen atom, the solution gives the possible energy states the electron can occupy [and the corresponding wave function(s) (ψ) (which in fact are the mathematical functions) of the electron associated with each energy state].

The probability of finding an electron at a point within an atom is proportional to the |ψ|² at that point.

|ψ|² is known as probability density and is always positive.

From the value of |ψ|² at different points within an atom, it is possible to predict the region around the nucleus where electron will most probably be found.

These quantized energy states and corresponding wave functions which are characterized by a set of three quantum numbers (principal quantum number n, azimuthal quantum number l and magnetic quantum number m_l) arise as a natural consequence in the solution of the Schrödinger equation.

According to the quantum mechanical model of the atom, the electron distribution of an atom containing a number of electrons is divided into shells. The shells, in turn, are thought to consist of one or more subshells and subshells are assumed to be composed of one or more orbitals, which the electrons occupy.

Orbitals and Quantum Numbers

A large number of orbitals are possible in an atom.

Qualitatively these orbitals can be distinguished by their size, shape and orientation.

An orbital of smaller size means there is more chance of finding the electron near the nucleus. Similarly shape and orientation mean that there is more probability of finding the electron along certain directions than along others.

Atomic orbitals are precisely distinguished by quantum numbers. Each orbital is designated by three quantum numbers labelled as n, l and m_l.

Principal quantum number ‘n’:

It is a positive integer with value of n = 1,2,3....... .

The principal quantum number determines the size and to large extent the energy of the orbital.

The principal quantum number also identifies the shell.

With the increase in the value of ‘n’, the number of allowed orbital increases and is given by ‘n²’.

All the orbitals of a given value of ‘n’ constitute a single shell of atom and are represented by the following letters:

n          = 1     2      3      4 ............

Shell   = K     L     M     N ............

Size of an orbital increases with increase of principal quantum number ‘n’.

Azimuthal quantum number. ‘l’:

It is also known as orbital angular momentum or subsidiary quantum number.

It defines the three-dimensional shape of the orbital. It also defines energy of orbital to some extent. For a given value of n, l can have n values ranging from 0 to n – 1, that is, for a given value of n, the possible value of l are : l = 0, 1, 2, .......... (n–1)

For example, when n = 1, value of l is only 0. For n = 2, the possible value of l can be 0 and 1. For n = 3, the possible l values are 0, 1 and 2.

Each shell consists of one or more subshells or sub-levels. The number of subshells in a principal shell is equal to the value of n.

For example in the first shell (n = 1), there is only one sub-shell which corresponds to l = 0. There are two sub-shells (l = 0, 1) in the second shell (n = 2), three (l = 0, 1, 2) in third shell (n = 3) and so on. Each sub-shell is assigned an azimuthal quantum number (l).

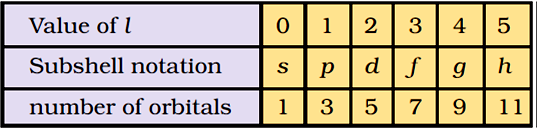
Sub-shells corresponding to different values of l are represented by the following symbols.

Value for l:	0	1	2	3	4	5	…
Notation for sub-shell:	s	P	d	F	g	h	…

Table below shows the permissible values of ‘l’ for a given principal quantum number and the corresponding sub-shell notation.

Magnetic orbital quantum number, ‘ml’:

It gives information about the spatial orientation of the orbital with respect to standard set of co-ordinate axis.

For any sub-shell (defined by ‘l’ value) 2l + 1 values of ml are possible and these values are given by:

m_l = – l, – (l –1), – (l–2)... 0, 1... (l – 2), (l–1), l

Thus for l = 0, the only permitted value of m_l = 0, [2(0) + 1 = 1, one ‘s’ orbital]. For l = 1, m_l can be –1, 0 and +1 [2(1) + 1 = 3, three ‘p’ orbitals]. For l = 2, m_l = –2, –1, 0, +1 and +2, [2(2) + 1 = 5, five ‘d’ orbitals]. It should be noted that the values of m_l are derived from l and that the value of l are derived from n.

Each orbital in an atom, therefore, is defined by a set of values for n, l and m_l. An orbital described by the quantum numbers n = 2, l = 1, m_l = 0 is an orbital in the p subshell of the second shell.

The following chart gives the relation between the sub-shell and the number of orbitals associated with it.

Electron spin quantum number (ms):

An electron spins around its own axis, much in a similar way as earth spins around its own axis while revolving around the sun.

In other words, an electron has, besides charge and mass, intrinsic spin angular quantum number.

Spin angular momentum of the electron — a vector quantity, can have two orientations relative to the chosen axis. These two orientations are distinguished by the spin quantum numbers m_s which can take the values of +½ or –½. These are called the two spin states of the electron and are normally represented by two arrows, ↑ (spin up) and ↓ (spin down).

Two electrons that have different m_s values (one +½ and the other –½) are said to have opposite spins.

An orbital cannot hold more than two electrons and these two electrons should have opposite spins.

To sum up, the four quantum numbers provide the following information:

i) n defines the shell, determines the size of the orbital and also to a large extent the energy of the orbital.

ii) There are n subshells in the nth shell. l identifies the subshell and determines the shape of the orbital.

There are (2l + 1) orbitals of each type in a subshell, that is, one ‘s’ orbital (l = 0), three p orbitals (l = 1) and five d orbitals (l = 2) per subshell. To some extent l also determines the energy of the orbital in a multi-electron atom.

iii) m_l designates the orientation of the orbital. For a given value of l, ml has (2l + 1) values, the same as the number of orbitals per subshell. It means that the number of orbitals is equal to the number of ways in which they are oriented.

iv) m_s refers to orientation of the spin of the electron.

Shapes of Atomic Orbitals

The square of the wave function (i.e., ψ²) at a point gives the probability density of the electron at that point. The variation of ψ² as a function of r for 1s and 2s orbitals is given in figure below.

Nodes: (or Radial nodes)

Note that for 1s orbital the probability density is maximum at the nucleus and it decreases sharply as we move away from it.

On the other hand, for 2s orbital the probability density first decreases sharply to zero and again starts increasing.

After reaching a small maxima it decreases again and approaches zero as the value of r increases further. The region where this probability density function reduces to zero is called nodal surfaces or simply nodes.

In general, it has been found that ns-orbital has (n – 1) nodes (radial nodes), that is, number of nodes increases with increase of principal quantum number n. In other words, number of nodes for 2s orbital is one, two for 3s and so on.

Charge cloud diagrams:

The probability density variation can be visualised in terms of charge cloud diagrams. In these diagrams, the density of the dots in a region represents electron probability density in that region.

Boundary surface diagrams:

In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density |ψ|² is constant.

In principle many such boundary surfaces may be possible. However, for a given orbital, only that boundary surface diagram of constant probability density is taken to be good representation of the shape of the orbital which encloses a region or volume in which the probability of finding the electron is very high, say, 90%.

The boundary surface diagram for 1s and 2s orbitals are given in the figure below.

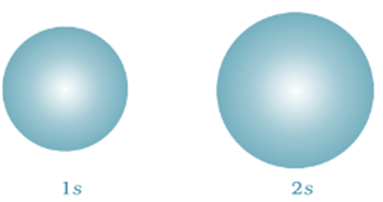
The size of the s orbital increases with increase in n, that is, 4s > 3s > 2s > 1s and the electron is located further away from the nucleus as the principal quantum number increases.

Boundary surface diagrams for three 2p orbitals (l = 1) are shown in the figure below.

Because there are three possible values of m_l, there are, therefore, three p orbitals whose axes are mutually perpendicular.

For l = 2, the orbital is known as d-orbital and the minimum value of principal quantum number (n) has to be 3. as the value of l cannot be greater than n – 1. There are five m_l values (–2, –1, 0, +1 and +2) for l = 2 and thus there are five d orbitals. The boundary surface diagrams of d orbitals are shown in the figure below.

The five d-orbitals are designated as d_xy, d_xz, d_yz, d_x2-y2, d_z2. The shapes of the first four d-orbitals are similar to each other, where as that of the fifth one, d_z2, is different from others, but all five 3d orbitals are equivalent in energy. The d orbitals for which n is greater than 3 (4d, 5d...) also have shapes similar to 3d orbital, but differ in energy and size.

Angular nodes:

Besides the radial nodes (i.e., probability density function is zero), the probability density functions for the np and nd orbitals are zero at the plane (s), passing through the nucleus (origin). For example, in case of p_z orbital, xy-plane is a nodal plane, in case of d_xy orbital, there are two nodal planes passing through the origin and bisecting the xy plane containing z-axis.

These are called angular nodes and number of angular nodes are given by ‘l’, i.e., one angular node for p orbitals, two angular nodes for ‘d’ orbitals and so on.

Total number of nodes:

The total number of nodes are given by (n – 1), i.e., sum of l angular nodes and (n – l – 1) radial nodes.

Shielding:

The stability of an electron in multi-electron atom is because total attractive interactions are more than the repulsive interactions amongst electrons. In general, the repulsive interaction of the electrons in the outer shell with the electrons in the inner shell are more important.

The attractive interaction of an electron increases with increase of positive charge (Ze) on the nucleus.

Due to the presence of electrons in the inner shells, the electron in the outer shell will not experience the full positive charge on the nucleus (Ze), but will be lowered due to the partial screening of positive charge on the nucleus by the inner shell electrons. This is known as the shielding of the outer-shell electrons from the nucleus by the inner shell electrons, and the net positive charge experienced by the electron from the nucleus is known as effective nuclear charge (Z_effe).

Despite the shielding of the outer electrons from the nucleus by the inner shell electrons, the attractive force experienced by the outer shell electrons increase with increase of nuclear charge.

Effectiveness of shielding effect:

Both the attractive and repulsive interactions depend upon the shell and shape of the orbital in which the electron is present.

For example, being spherical in shape, the s orbital shields the electrons from the nucleus more effectively as compared to p orbital.

Similarly, because of difference in their shapes, p orbitals shield the electrons from the nucleus more than the d orbitals, even though all these orbitals are present in the same shell.

Further due to spherical shape, s orbital electron spends more time close to the nucleus in comparison to p orbital and p orbital spends more time in the vicinity of nucleus in comparison to d orbital. In other words, for a given shell (principal quantum number), the Z_eff experienced by the orbital decreases with increase of azimuthal quantum number (l), that is, the s orbital will be more tightly bound to the nucleus than p orbital and p orbital in turn will be better tightly bound than the d orbital.

Energies of Orbitals:

The energy of s orbital will be lower (more negative) than that of p orbital and that of p orbital will be less, than that of d orbital and so on.

Since the extent of shielding of the nucleus is different for different orbitals, it leads to the splitting of the energies of the orbitals within the same shell (or same principal quantum number), that is, energy of the orbital, as mentioned earlier, depends upon the values of n and l.

Mathematically, the dependence of energies of the orbitals on n and l are quite complicated but one simple rule is that of combined value of n and l.

The lower the value of (n + l) for an orbital, the lower is its energy.

If two orbitals have the same value of (n + l), the orbital with lower value of n will have the lower energy.

It may be noted that different subshells of a particular shell have different energies in case of multi-electrons atoms. However, in hydrogen atom, these have the same energy. Lastly it may be mentioned here that energies of the orbitals in the same subshell decrease with increase in the atomic number (Z_eff). For example, energy of 2s orbital of hydrogen atom is greater than that of 2s orbital of lithium and that of lithium is greater than that of sodium and so on, that is,

E_2s(H) > E_2s(Li) > E_2s(Na) > E_2s(K)

Quantum Numbers – Summarised

Pauli Exclusion Principle:

No two electrons in an atom can have the same four quantum numbers.

It can also be stated as 'an orbital can have maximum two electrons and they must be of opposite spin quantum numbers'.

Aufbau Principle:

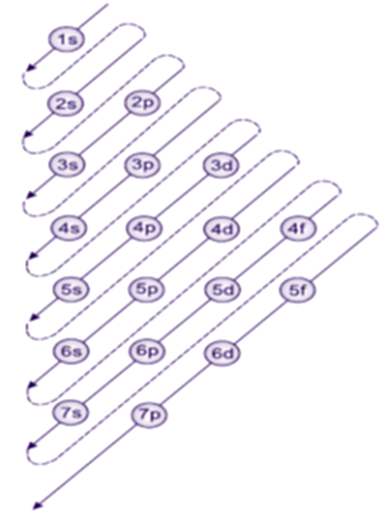
In the ground state, electrons are filled in the various orbitals in an increasing order of their energies, i.e. orbital having lowest energy will be filled first and the orbital having highest energy will be filled last.

 (i) Orbitals are filled in the order of increasing value of (n + l). This means that. Between 3d and 4s orbitals, 4s (n + l = 4 + 0 = 4) is filled before 3d (n + l = 3 + 2 = 5).

(ii) If two orbitals have the same value of (n + l), the one with lower 'n' will be filled first. Thus, between 2p (n + l = 2 + 1 = 3) and 3s (n + l = 3 + 0 = 3), 2p will be filled before 3s.

By applying aforesaid rules, Aufbau stated the order of filling up of electrons in the orbitals as follows:

Hund’s Rule of Maximum Multiplicity:

Pairing of electrons in the orbitals belonging to the same subshell (e.g. p, d or f) does not take place until each orbital belonging to that subshell has got one electron each i.e., it is singly occupied.

Electronic Configuration of Atoms:

The distribution of electrons into orbitals of an atom is called its electronic configuration.

The electronic configuration of different atoms can be represented in two ways. For example :

(i) s^a p^b d^c ...... notation  (a, b, c, … represent number of electrons in respective subshells)

E.g., The electronic configuration of the hydrogen atom is 1s¹ meaning that it has one electron in the 1s orbital. The second electron in helium (He) can also occupy the 1s orbital. Its configuration is, therefore, 1s².

The third electron of lithium (Li) is not allowed in the 1s orbital because of Pauli exclusion principle. It, therefore, takes the next available choice, namely the 2s orbital.

Hence electronic configuration of next few elements will be:

(ii) Orbital diagram

In this notation, each orbital of the subshell is represented by a box and the electron is represented by an arrow (↑) a positive spin or an arrow (↓) a negative spin.

Orbital electronic configuration of hydrogen and Helium will be

The advantage of second notation over the first is that it represents all the four quantum numbers.

The orbital picture of next few elements can be represented as follows:

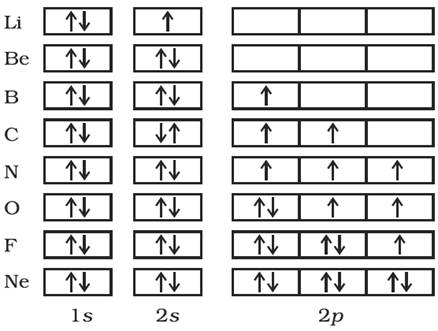
Chromium (24) and Copper (29) have five and ten electrons in 3d orbitals rather than four and nine as their position would have indicated with two-electrons in the 4s orbital. The reason is that fully filled orbitals and half-filled orbitals have extra stability (that is, lower energy).

Thus p³, p⁶, d⁵, d¹⁰, f⁷, f¹⁴ etc. configurations, which are either half-filled or fully filled, are more stable. Chromium and copper therefore adopt the d⁵ and d¹⁰ configuration

Stability of Completely Filled and Half-Filled Subshells:

In certain elements such as Cu, or Cr, where the two subshells (4s and 3d) differ slightly in their energies, an electron shifts from a subshell of lower energy (4s) to a subshell of higher energy (3d), provided such a shift results in all orbitals of the subshell of higher energy getting either completely filled or half filled.

The valence electronic configurations of Cr and Cu, therefore, are 3d⁵ 4s¹ and 3d¹⁰ 4s¹ respectively and not 3d⁴ 4s² and 3d⁹ 4s².

Cr (24): [Ar] 4s¹ 3d⁵

Cu (29): [Ar] 4s¹ 3d¹⁰

Reasons for Stability of Completely-Filled and Half-Filled Sub-shells:

1. Symmetrical distribution of electrons:

It is well known that symmetry leads to stability. The completely filled or half-filled subshells have symmetrical distribution of electrons in them and are therefore more stable.

2. Exchange Energy:

When two or more electrons with the same spin, in the degenerate orbitals of a subshell, exchange their positions, then the energy released due to this exchange is called exchange energy.

Details about the exchange energy will be dealt with in higher classes.

The greater the number of exchanges, the greater will be exchange energy and more will be stability.

The number of exchanges, that can take place, is maximum when the subshell is either half-filled or completely filled. As a result, the exchange energy is maximum and so is the stability.

Note that the exchange energy is at the basis of Hund’s rule that electrons which enter orbitals of equal energy have parallel spins as far as possible.

In other words, the extra stability of half-filled and completely filled subshell is due to:

(i) relatively small shielding

(ii) smaller coulombic repulsion energy

(iii) larger exchange energy.

Online Tuitions & Self-Study Courses for Grade 6 to 12 & JEE / NEET