Algebraic Expressions

Any expression involving constant, variable and some operations like addition, multiplication etc is called Algebraic Expression.

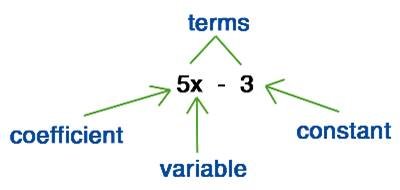
A variable is an unknown number and generally, it is represented by a letter like x, y, z, a, m etc.

Any number without any variable is called Constant.

A number followed by a variable is called Coefficient of that variable.

A term is any number or variable separated by operators.

Equation

A statement which says that the two expressions are equal is called Equation.

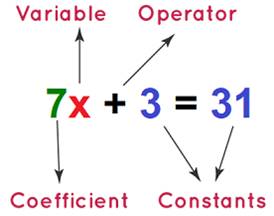
Linear Expression

A linear expression is an expression whose highest power of the variable is one only.

Example: 2m − 7, 5 + 8y, 7x etc.

The expressions like x² + 3, y² + 5y + 6 are not the linear expressions as their highest power of the variable is greater than 1.

Linear Equations

The equation of a straight line is the linear equation. It could be in one variable or two variables.

Linear Equation in One Variable

If there is only one variable in the equation then it is called a linear equation in one variable.

The general form is

    ax + b = c, where a, b and c are real numbers and a ≠ 0.

Example:

    k + 7 = 11

    n – 5 = 23

These are called linear equations in one variable because the highest degree of the variable is one and there is only one variable.

Some Important points related to Linear Equations

There is an equality sign in the linear equation. The expression on the left of the equal sign is called the LHS (left−hand side) and the expression on the right of the equal sign is called the RHS (right−hand side).

In the linear equation, the LHS is equal to RHS but this happens for some values only and these values are the solution of these linear equations.

Graph of the Linear Equation in One Variable

We can mark the point of the linear equation in one variable on the number line.

x = 2 can be marked on the number line as follows:

Solving Equations which have Linear Expressions on one Side and Numbers on the other Side

There are two methods to solve such type of problems−

1. Balancing Method

In this method, we have to add or subtract with the same number on both the sides without disturbing the balance to find the solution.

Example: Find the solution for 3y – 5 = 25

Solution: Step 1: We need to add 5 to both the sides so that the numbers and variables come on the different sides without disturbing the balance.

    3y – 5 + 5 = 25 + 5

    3y = 30

Step 2: Now to balance the equation, we need to divide by 3 into both the sides.

    3y/3 = 30/3

    y = 10

Hence y = 10 is the solution of the equation.

Validation:

    3y – 5 = 25

    3(10) – 5 = 25

    30 − 5 = 25

    25 = 25

Here, LHS = RHS.

2. Transposing Method

In this method, we need to transpose or transfer the constants or variables from one side to another until we get the solution. When we transpose the terms, the sign will get changed.

Example: Find the solution for 2z − 11 = 17.

Solution:

Step 1: We transpose − 11 from LHS to RHS so that all the constants come in the same side.

    2z = 17 + 11 (sign will get changed)

    2z = 28

Step 2: Now divide both the sides by 2.

    2z/2 = 28/2

    z = 14

Here z = 14 is the solution of the equation.

Some Applications of Linear Equation

We can use the concept of linear equations in our daily routine also. There are some situations where we need to use the variable to find the solution. Like,

What number should be added to 53 to get 85?

If the sum of two numbers is 350 and one of the numbers is 123 then what will be the other number?

Example: What is the breadth of the rectangle whose perimeter is 96 cm and the length is 33 cm?

Solution:

Let the breadth of the rectangle be ‘b’.

Perimeter rectangle = 2 (Length + Breadth)

    96 = 2 ( 33 + b )

    96 = 66 + 2b

Now, this is a linear equation with variable b.

First we subtract 66 from both sides

    96 – 66 = 66 + 2b – 66

    30 = 2b

We need to divide both sides by 2 to find the solution.

    30/2 = 2b/2

    15 = b

or b = 15 cm

Hence the breadth of the rectangle is 15 cm.

Solving Equations having the Variable on both Sides

As the equation can have the variable on both the sides also so we should know how to solve such problems.

In this type of problems, we need to bring all the constants on one side and all the terms having variables on the other side. Then they can be solved easily.

Example: Find the solution of 2x − 3 = 6 − x.

Solution:

Step 1: Bring all the terms including variable x on LHS and the constants on the RHS.

    2x + x = 6 + 3 (sign will change while changing the position of the terms)

Step 2: Solve the equation

    3x = 9

Step 3: Divide both the sides by 3 to get the solution.

    3x/3 = 9/3

    x = 3

Hence the solution of the equation is x = 3.

Example: Deepika’s age is four times that of her younger brother. Five years back her age was 9 times her brother’s age. Find their present ages.

Solution:

Let the Deepika’s brother age = x

Deepika’s age = 4x (as her age is 4 times that of her younger brother)

Five years back her age was = 9(x – 5) which is equal to 4x – 5

9(x – 5) = 4x – 5

9x – 45 = 4x – 5

9x – 4x = – 5 + 45 (by transferring the variable and constants on different sides)

5x = 40

x = 40/5 = 8

Deepika’s brother age = x = 8 years

Deepika’s age = 4x = 4(8) = 32 years.

Reducing Equations to Simpler Form

When linear equations are in fractions then we can reduce them to a simpler form by

Taking the LCM of the denominator

Multiply the LCM on both the sides, so that the number will reduce without the denominator and we can solve them by the above methods.

Example: Solve the linear equation

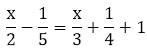
Solution:
As the equation is in complex form, we have to reduce it into a simpler form.

Step 1: Take the L.C.M. of the denominators, 2, 3, 4, and 5, which is 60.
Step 2: Multiply both the sides by 60,

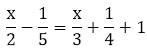
30x −12 = 20x + 15 + 60

Step 3. Bring all the variables on the LHS and all the constants on the RHS

30x − 20x = 15 + 12 + 60

10x = 87

Step 4: Dividing both the sides by 10

x = 8.7

Example:

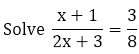
Solution: This is not a linear equation but can be reduced to linear form

Step 1: Multiply both the sides by (2x + 3).

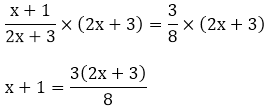
Now, this is a linear equation.

Step 2: Multiply both the sides by 8.

8(x + 1) = 3(2x + 3)

8x + 8 = 6x + 9

8x − 6x = 9 − 8

2x = 1

x = 1/2

Hence the solution for the equation is x = 1/2.

Example: Simplify the equation  .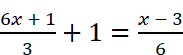

Solution:

     
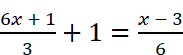
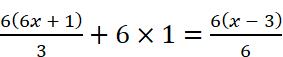       [Multiplying both sides by 6]
⇒ 2(6x + 1) + 6 = (x − 3)
⇒ 12x + 2 + 6 = x – 3     [Opening the brackets]
⇒ 12x + 8 = x − 3
⇒ 12x – x + 8 = −3         [Transposing x to LHS]
⇒ 11x + 8 = −3
⇒ 11x = −3 −8
⇒ 11x = −11
⇒ x = −1 (required solution)

Validation of the result:

    LHS: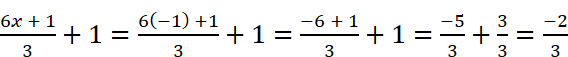  

    RHS: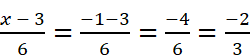  

Hence, LHS = RHS.

 

Online Tuitions & Self−Study Courses for Grade 6 to 12 & JEE / NEET