A shape is said to be symmetric if there exists an imaginary line passing through that divides the shape into halves and that these halves overlap each other completely.

If we fold the shape about the imaginary line then, if they overlap each other completely the shape is symmetric, if not, then it is asymmetric.

Symmetry defines that one shape is exactly like the other shape when it is moved, rotated, or flipped.

If you are told to cut out a ‘heart’ from a piece of paper, you can simply fold the paper, draw one-half of the heart at the fold and cut it out to find that the other half exactly matches the first half. The heart carved out is an example of symmetry.

 

“Symmetry is a mirror image”. When an image looks identical to the original image after the shape is being turned or flipped, then it is called symmetry. It exists in patterns.

 

Line of Symmetry

 

The imaginary line or axis along which you fold a figure to obtain the symmetrical halves is called the line of symmetry. It basically divides an object into two mirror-image halves. The line of symmetry can be vertical, horizontal or diagonal. There may be one or more lines of symmetry.

·        1 line: Figure is symmetrical only about one axis. It may be horizontal or vertical. E.g., the word ATOYOTA has one axis of symmetry along the axis passing through Y.

A butterfly has one line of symmetry.

 

 

·        2 lines: Figure is symmetrical only about two lines. The lines may vertical and horizontal lines as viewed in the letters H and X.

 

·        Infinite lines: Some figures have not one or two, but infinite lines passing through the centre, and the figure is still symmetrical. Example: a circle.

 

 

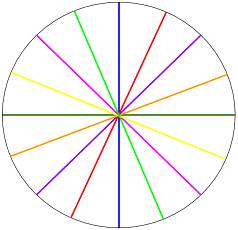
Types of Symmetry

 

Symmetry may be viewed when you flip, slide or turn an object. There are four types of symmetry that can be observed in various situations, they are:

 

Translation Symmetry:

If the object is translated or moved from one position to another, the same orientation in the forward and backward motion is called translational symmetry. In other words, it is defined as the sliding of an object about an axis. This can be observed clearly from the figure given below, where the shape is moved forward and backward in the same orientation by keeping the fixed axis.

 

 

Rotational Symmetry:

If a figure is rotated around a centre point and it still appears exactly as it did before the rotation, it is said to have rotational symmetry. A number of shapes like squares, circles, regular hexagon, etc. have rotational symmetry.

There are many shapes you will see in geometry which are symmetrical rotationally, such as:

·        Equilateral triangles

·        Squares

·        Rectangles

·        Circles

·        Regular Polygons

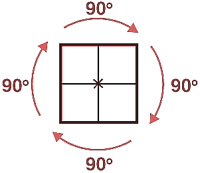
Centre of Rotation

 

For a figure or object that has rotational symmetry, the fixed point around which the rotation occurs is called the centre of rotation. Example: the centre of rotation of a windmill in the centre of the windmill from which its blades originate.

 

Angle of Rotational Symmetry

 

For a figure or object that has rotational symmetry, the angle of turning during rotation is called the angle of rotation. Example: when a square is rotated by 90 degrees, it appears the same after rotation. So, the angle of rotation for a square is 90 degrees.

In the same way, a regular hexagon has an angle of symmetry as 60 degrees,  a regular pentagon has 72 degrees, and so on.

 

Order of Rotational Symmetry

 

The number of positions in which a figure can be rotated and still appears exactly as it did before the rotation, is called the order of symmetry. For example, a star can be rotated 5 times along its tip and look at the same every time. Hence, its order of symmetry is 5.

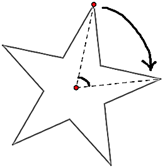
If we consider the order of symmetry for regular hexagon it is equal to 6, since it has 6 equal sides and is rotated with an angle of 60 degrees.

 

Rotational Symmetry Letters

 

There are many capital letters of English alphabets which has symmetry when they are rotated clockwise or anticlockwise about an axis. Some of them are: Z, H, S, N and O. When these letters are rotated 180 degrees clockwise or anticlockwise the letters appears to be same.

 

Examples of Rotational Symmetry

 

·        The recycle logo has an order of symmetry of 3.

 

·        The paper windmill has an order of symmetry of 4.

 

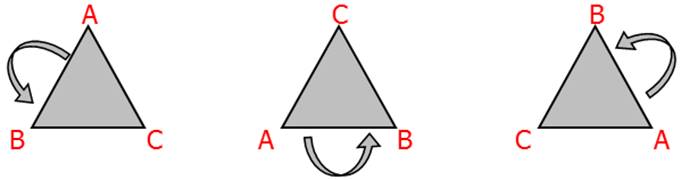
·        The triangle has an order of symmetry of 3.

 

·        The Swastik symbol has an order of symmetry of 4.

 

Reflection Symmetry

 

Reflection symmetry is a type of symmetry which is with respect to reflections. Reflection symmetry is also known as line symmetry or mirror symmetry. It states that if there exists at least one line that divides a figure into two halves such that one-half is the mirror image of the other half.

• The line where a mirror can be kept so that one-half appears as the reflection of the other is called the line of symmetry.
• A figure can have one or more lines of reflection symmetry.
• The line of symmetry can be in any direction.

 

Examples of Reflection Symmetry

 

·        Regular polygons of N sides have N lines of symmetry.

 

Triangle: 3 Lines of Symmetry

 

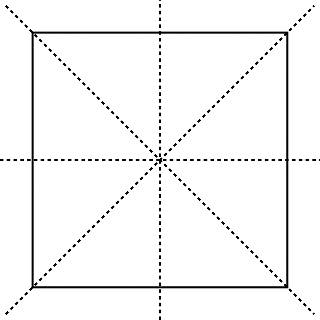
Square: 4 Lines of Symmetry

 

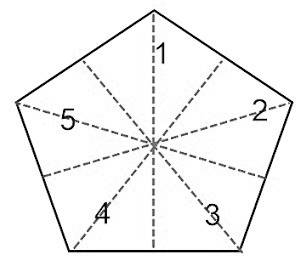
Pentagon: 5 Lines of Symmetry

 

·        A rectangle has a vertical and a horizontal line of symmetry.

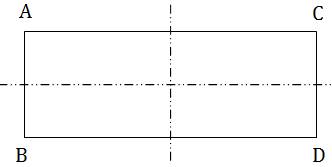
Rectangle: 2 Lines of Symmetry

 

Rectangle is not symmetrical across its diagonal.

 

·        Reflection symmetry is also observed in inkblot paper. Pour a little ink and water drop on one side of a paper. Fold the paper into two halves and press it with your palm. Unfold the paper to see the symmetric pattern along the line of the fold. The line of the fold is the axis of reflection.

 

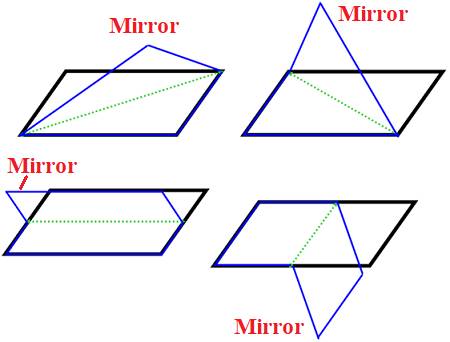
Is Parallelogram Symmetrical?

 

·        A parallelogram is not symmetrical along any of the axes of reflection.

 

 

Solved Examples

 

Example 1: If the figure below follows a reflexive or line of symmetry, then complete the figure.

Solution:

Given that, the figure has a line of symmetry.

That means, the second half (i.e. missing part) of the figure will be exactly the same as the given.

Thus, the complete figure is:

 

Example 2: Identify the shapes which do not have rotational symmetry from the below figure.

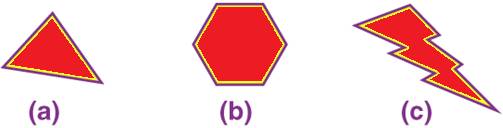
Solution:

As we know, rotational symmetry is a type of symmetry, when we rotate a shape in a particular direction, the resultant shape is exactly the same as the original shape.

Thus, from the given figure (a) and (c) do not have a rotational symmetry.

 

A Little Bit Extra

Glide Symmetry: The combination of both translation and reflection symmetry is defined as the glide symmetry. A glide reflection is commutative in nature. If we change the combination’s order, it will not alter the output of the glide reflection.