Algebra

Algebra is a part of mathematics in which the letters and symbols are used to represent numbers in equations. It helps us to study about unknown quantities.

Algebra as Patterns

Number patterns

If a natural number is denoted by n, then its successor is (n + 1).

Example: Successor of n = 10 is n + 1 = 11.

If a natural number is denoted by n, then 2n is an even number and (2n + 1) is an odd number.

Example: If n = 10, then 2n = 20 is an even number and 2n + 1 = 21 is an odd number.

Matchstick Patterns

No. of matchsticks used to make 1^st square = 4

No. of matchsticks used to make 2^nd square = 7

No. of matchsticks used to make 3^rd square = 10

So, the pattern that we observe here is 3n + 1

With this pattern, we can easily find the number of matchsticks required in any number of squares.

Example

How many matchsticks will be used in the 50^th figure?

Solution

3n + 1

3 × 50 + 1

=  151 matchsticks

Patterns in Geometry

·        Some geometrical figures follow patterns which can be represented by algebraic expressions.
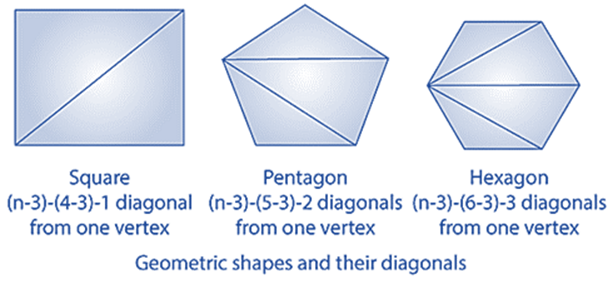
Example: Number of diagonals we can draw from one vertex of a polygon of n sides is (n – 3) which is an algebraic expression.

Constant

Constant is a quantity which has a fixed value. In 2x + 5, 5 is the constant.

Variables

Variable refers to the unknown quantities that can change or vary and are represented using the lowercase letter of the English alphabets.

One such example of the same is the rule that we used in the matchstick pattern 3n + 1

Here the value of n is unknown and it can vary from time to time.

Examples of Variables

·        We can use any letter as a variable, but only lowercase English alphabets.

·        Numbers cannot be used for the variable as they have a fixed value.

·        They can also help in solving some other problems.

Example

Gita wanted to buy story books from a bookstall. She wanted to buy 3 books for herself, 2 for her brother and 4 for 2 of her friends. Each book cost Rs.15.how much money she should pay to the shopkeeper?

Solution

Cost of 1 book = Rs.15

We need to find the cost of 9 books.

No. of notebooks	1	2	3	4	…….	a	….....
Total cost	15	30	45	60	…….	15a	…….

In the current situation, variable a stands for 9

Therefore,

Cost of 9 books = 15 × 9

= 135

Therefore, Gita needs to pay Rs.135 to the shopkeeper of the bookstall.

Example

Meena has 2 chocolates more than Tina. Form an expression for the statement.

Solution

Chocolates that Tina have can be represented using a variable (x)

Chocolates that Meena have = chocolates that Tina have + 2

Chocolates with Meena = x + 2

Alternate Solution

Chocolates that Meena have can be represented using a variable (y)

Chocolates that Tina has = chocolates that Meena have − 2

Chocolates with Tina = y − 2

Use of Variables in Common Rules (Geometry)

1. Perimeter of Square

The perimeter of a square = Sum of all sides

           = 4 × side

           = 4s

Thus, p = 4s

Here, s is variable, so the perimeter changes as the value of side change.

2. Perimeter of Rectangle

Perimeter of rectangle = 2(length + breadth)

           = 2 (l + b) or 2l + 2b

Thus, p + 2 × (l + b) or 2l + 2b

Where, l and b are variable and the value of perimeter changes with the change in l and b.

Use of Variables in Common Rules (Arithmetic)

1. Commutativity of Addition

           5 + 4 = 9

           4 + 5 = 9

Thus, 5 + 4 = 4 + 5

This is the commutative property of addition of the numbers, in which the result remains the same even if we interchanged the numbers.

           a + b = b + a

Here, a and b are different variables.

Example

    a = 16 and b = 20

According to commutative property

    16 + 20 = 20 + 16

    36 = 36

2. Commutativity of Multiplication

    8 × 2 = 16

    2 × 8 = 16

Thus, 8 × 2 = 2 × 8

This is the commutative property of multiplication, in which the result remains the same even if we interchange the numbers.

    a × b = b × a

Here, a and b are different variables.

Example

    18 ×12 = 216, 12 ×18 = 216

Thus, 18 × 12 = 12 × 18

3. Distributivity of Numbers

    6 × 32

It is a complex sum but there is an easy way to solve it. It is known as the distributivity of multiplication over the addition of numbers.

           6 × (30 + 2)

    =    180 + 12

    =    192

Thus, 6 × 32 = 192

    A × (b + c) = a × b + a × c

Here, a, b and c are different variables.

4. Associativity of Addition

This property states that the result of the numbers added will remain same regardless of their grouping.

    (a + b) + c = a + (b + c)

Example

    (4 + 2) + 7 = 4 + (2 + 7)

    6 + 7 = 4 + 9

    13 = 13

Expressions

Arithmetic expressions may use numbers and all operations like addition, subtraction, multiplication and division

Example

    2 + (9 – 3), (4 × 6) – 8 etc…

    (4 × 6) – 8 = 24 – 8

    = 16

Expressions with variable

We can make expressions using variables like 2m, 5 + t etc…..

An expression containing variable/s cannot be analyzed until its value is given.

Example

Find 3x – 12 if x = 6

Solution

    (3 × 6) – 12

= 18 – 12

= 5

Thus,

    3x – 12 = 5

Formation of Expressions

Statement	Expression
y subtracted from 12	12 - y
x multiplied by 6	6x
t Multiplied by 4, and then subtract 5 from the product.	4t - 5

Terms of an Expression

Parts of an expression which are formed separately first and then added or subtracted, are known as terms.
Terms 2x and 5 can be added to form the expression (2x + 5).

Factors of a term

Parts of an expression which are formed separately first and then added or subtracted, are known as terms.

·        Factors of a term are quantities which cannot be further factorised.

·        In the above-given example, factors of the term 2x are 2 and x.

Coefficient of a term

The numerical factor of a term is called the coefficient of the term.
In the above-given example, 2 is the coefficient of the term 2x.
To know more about Term, factor and Coefficient, visit here.

Like terms

Terms having the same variables are called like terms.>
Example: 8xy and 3xy are like terms.

Unlike terms

Terms having different variables are called, unlike terms.
Example: 7xy and -3x are unlike terms.

Monomial, Binomial, Trinomial and Polynomial Terms

Practical use of Expressions

Example

3 boys go to the theatre. The cost of the ticket and popcorn is ₹ 33 and ₹15 respectively. What is the cost per person?

Solution

Let’s say,

 x = cost of ticket per person

 y = cost of popcorn/person

Total cost of the movie (ticket + popcorn) per person = x + y

Total cost of ticket + popcorn for 3 boys = 3(x + y)

    = 3 (33 + 15)

    = 3 (48)

    = 144

Hence the total cost of movie ticket and popcorn for 3 boys is ₹ 144.

Addition and Subtraction of like terms

Sum of two or more like terms is a like term.

Its numerical coefficient will be equal to the sum of the numerical coefficients of all the like terms.
Example:  8y + 7y = ?           

             8y
     + 7y
___________
   (8 + 7)y = 15y
____________

Difference between two like terms is a like term.

Its numerical coefficient will be equal to the difference between the numerical coefficients of the two like terms.
Example: 11z − 8z = ?

      11z

          − 8z

__________

   (1 − 8)z = 3z
___________

Addition and Subtraction of unlike terms

·        For adding or subtracting two or more algebraic expressions, like terms of both the expressions are grouped together and unlike terms are retained as it is.

·        Adding −5x² + 12xy and 7x² + xy + 7x is shown below:

       −5x² + 12xy
     7x² +  xy   +  7x
   ______________
     2x²  +  13xy + 7x
   ______________

·        Subtracting of −5x² + 12xy and 7x² + xy + 7x is shown below:

         −5x² + 12xy
    −7x²  +  xy  +  7x
    _______________

         12x² + 11xy − 7x
    _______________

Algebraic expressions in perimeter  and area formulae

·        Algebraic expressions can be used in formulating perimeter of figures.
Example: Let L be the length of one side then, the perimeter of :

1.    An equilateral triangle = 3L.

2.    A square = 4L.

3.    A regular pentagon = 5L.

·        Algebraic expressions can be used in formulating area of figures.
Example: Area of :

1.    Square = l² where l is the side length of the square.

2.    Rectangle = l × b, where l and b are lengths and breadth of the rectangle.

3.    Triangle = 1/2 b × h where b and h are base and height of the triangle.

Equation

If we use the equal sign between two expressions then they form an equation.

An equation satisfies only for a particular value of the variable.

The equal sign says that the LHS is equal to the RHS and the value of a variable which makes them equal is the only solution of that equation.

Example

    3 + 2x = 13

    5m – 7 = 3

        p/6 = 18

If there is the greater then or less than sign instead of the equal sign then that statement is not an equation.

Some examples which are not an equation

    23 + 6x  > 8

    6f – 3 < 24

The Solution of an Equation

The value of the variable which satisfies the equation is the solution to that equation. To check whether the particular value is the solution or not, we have to check that the LHS must be equal to the RHS with that value of the variable.

Trial and Error Method

To find the solution of the equation, we use the trial and error method.

Example

Find the value of x in the equation 25 – x = 15.

Solution

Here we have to check for some values which we feel can be the solution by putting the value of the variable x and check for LHS = RHS.

Let’s take x = 5

    25 – 5 = 15

    20 ≠ 15

Hence, x = 5 is not the solution of that equation.

Let’s take x = 10

    25 – 10 = 15

    15 = 15

    LHS = RHS

Hence, x = 10 is the solution of that equation.