Algebraic Expression:
An algebraic expression is an expression built up from integer constants, variables, and the algebraic operations like addition, subtraction, multiplication, division, etc.
Variable:
A variable can take any value. Its value is not fixed.
Ex: x, y, z, p, q, …….., etc are variables.
Constant:
A constant has a fixed value.
Ex: 10, –20, 100, etc. are constant.
Variables and constants combine to make algebraic expressions.
Ex: 2x + 5, 7y – 10, etc are algebraic expressions.
An algebraic expression 2x + 5 is formed as:
First the variable x is multiplied to constant 2 and then adding the constant 5 to the product.
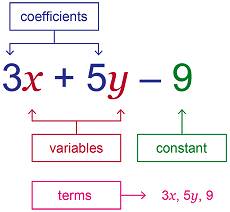
Terms of an Expression
Terms are added to form an expression.
Ex: terms 3x and 7 are added to form the expression 3x + 7
Again, the expression 2y2 – 7xy are formed by adding the terms
2y2 and –7xy i.e. 2y2 + (–7xy) = 2y 2 – 7xy
Factors of a term
A term is a product of its factors.
Let us take a term 2y2
The term 2y2 is a product of 2, y and y. Now, we say that 2, y and y are the factors of the term 2y2
Again the term – 7xy is a product of the factors –7, x and y.
Coefficient
The numerical factor is said to be the numerical coefficient or simply the coefficient of the term.
Ex: In the term 20y2, 20 is the coefficient of y2.
Again, in the term –3xyz, –3 is the coefficient of xyz.
In general, a coefficient may be either a numerical factor or an algebraic factor or a product of two or more factors.
Ex: In the term 7xy, 7 is the coefficient of xy, x is the coefficient of 7y and y is the coefficient of 7x.
In 5xy2, 5 is the coefficient of xy2, x is the coefficient of 5y2 and y2 is the coefficient of 5x.
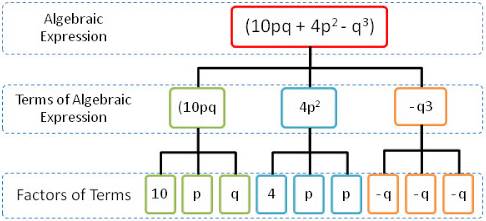
We can represent the terms and factors of an expression in an efficient way by using a tree diagram.
Ex: Let us take the expressions 10pq + 4p2 – q3 to draw the tree.
Like and Unlike Terms
Like terms are terms that have the same variables and powers. The coefficients do not need to match.
Ex: 8xy2 and −5xy2 are like terms because they have the same variables and power.
Unlike terms are terms that have not the same variables or powers.
Ex: 3abc and 3xyz are unlike terms because they have different variables.
Problem: Identify like terms in the following:
–xy2, –4yx2, 8x2, 2xy2, 7y, –11x2, –100x, –11yx, 20x2 y, –6x2, y, 2xy, 3x
Solution:
Like terms are:
(i) –xy2, 2xy2
(ii) –4yx2, 20x2y
(iii) 8x2, –11x2, –6x2
(iv) 7y, y
(v) –100x, 3x
(vi) –11yx, 2xy
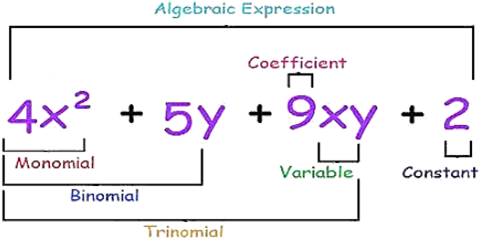
Monomials, Binomials, Trinomials and Polynomials
An expression with only one term is called a monomial.
Ex: 2x, 5xy, –3p, 4y2, –7, etc are called monomials.
An expression which contains two unlike terms is called a binomial.
Ex: p + 2q, m – 2n, x2 – y2, etc are called binomials.
An expression which contains three terms is called a trinomial.
Ex: a + b + 5, 2p + 3q – 5r, 3x2 – 5y + 10z are trinomials.
An expression which has one or more terms is called a polynomial. Thus a monomial, a binomial and a trinomial are all polynomials.
Addition and Subtraction of Algebraic Expressions
We can add and subtract the algebraic expressions as follows:
Adding and Subtracting like terms
Let we want to add 5x and 7x
Now, 5x + 7x = 5 × x + 7 × x
= (5 + 7) × x [Apply distributive Law]
= 12 × x
= 12x
So, 5x + 7x = 12x
Again let we want to add 3xy, 4xy and 7xy
Now, 3xy + 4xy + 7xy = 3 × xy + 4 × xy + 7 × xy
= (3 + 4 + 7) × xy
= 14 × xy
= 14xy
So, 3xy + 4xy + 7xy = 14xy
Thus, the sum of two or more like terms is a like term with a numerical coefficient equal to the sum of
the numerical coefficients of all the like terms.
Again we want to subtract 5p from 12 p
12p – 5p = 12 × p – 5 × p
= (12 – 5) × p
= 7 × p
= 7p
So, 12p – 5p = 7p
In the same way, we subtract 9pq from 15pq
So, 15pq – 9pq = 6pq
Thus, the difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.
Again unlike terms cannot be added or subtracted the way like terms are added or subtracted.
Ex: When x is added to 10 it gives (x + 10). Similarly, when 10 is subtracted from 7pq, it gives 7pq – 10
Adding and Subtracting general algebraic expressions
Let us take some examples:
Example: Add 5x + 7 and 2x + 10
Sum = (5x + 7) + (2x + 10)
= 5x + 7 + 2x + 10
= (5x + 2x) + (7 + 10)
= 7x + 17
Example: Subtract 24xy – 10y – 18x from 30xy + 12y + 14x
Subtraction = 30xy + 12y + 14x – (24xy – 10y – 18x)
= 30xy + 12y + 14x – 24xy + 10y + 18x
= 30xy – 24xy + 12y + 10y + 14x + 18x
= 6xy + 22y + 32x
Problem:
(a) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy ?
(b) What should be subtracted from 2a + 8b + 10 to get –3a + 7b + 16 ?
Answer:
(a) Let p should be added.
Then, according to question,
x2 + xy + y2 + p = 2x2 + 3xy
p = 2x2 + 3xy – (x2 + xy + y2)
p = 2x2 + 3xy – x2 – xy – y2
p = x2 + 2xy – y2
Hence, x2 + 2xy – y2 should be added.
(b) Let q should be subtracted.
Then, according to question,
2a + 8b + 10 – q = –3a + 7b + 16
–q = –3a + 7b + 16 – (2a + 8b + 10)
–q = –3a + 7b + 16 – 2a – 8b – 10
–q = –5a – b + 6
q = –(–5a – b + 6) [Multiply (–) sign on both side]
q = 5a + b – 6
Hence, 5a + b – 6 should be subtracted.
Finding the Value of an Expression
The value of an algebraic expression depends on the value of the variables which forms the expression.
There are many situations where we need to find the value of an expression, such as when we want to check whether a particular value of a variable satisfies a given equation or not.
Ex: Find the values of the following expressions for x = 5.
3x – 7
Answer:
Replace x with 5, we get
3x – 7 = 3 × 5 – 7 = 15 – 7 = 8
Ex: Calculate the following expression for x = 3 and z = 2
6z + 4x = ?
Answer: Replace x with 3 and z with 2 in the expression, we get
6z + 4x = 6 × 2 + 4 × 3 = 12 + 12 = 24
Problem: If m = 2, find the value of:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m2 – 2m – 7
(v) 5m/2 – 4
Answer:
Put m = 2, we get
(i) m – 2 = 2 – 2 = 0
(ii) 3m – 5 = 3 × 2 – 5 = 6 – 5 = 1
(iii) 9 – 5m = 9 – 5 × 2 = 9 – 10 = –1
(iv) 3m2 – 2m – 7 = 3 × 22 – 2 × 2 – 7
= 3 × 4 – 4 – 7
= 12 – 11
= 1
(v) 5m/2 – 4 = (5 × 2)/2 – 4
= 10/2 – 4
= 5 – 4
= 1
Using Algebraic Expressions – Formulas and Rules
Rules and formulas in mathematics are written in a concise and general form using algebraic expressions.
Perimeter Formula:
1. Let l be the length of the side of an equilateral triangle.
So, Perimeter of equilateral triangle = 3 × Length of side of equilateral triangle = 3l
2. Let l be the length of the side of a square.
So, Perimeter of equilateral triangle = 4 × Length of side of square = 4l
3. Let l be the length of the side of a regular pentagon.
So, Perimeter of equilateral triangle = 5 × Length of side of regular pentagon = 5l
Area formulas
1. If we denote the length of a square by l, then the area of the square = l2
2. If we denote the length of a rectangle by l and its breadth by b, then the area of the rectangle
= l × b = lb
3. If b stands for the base and h for the height of a triangle, then the area of the triangle
= (b × h)/2 = bh/2
Rules for number patterns:
1. If a natural number is denoted by n, its successor is (n + 1).
Ex: If n = 20, its successor is n + 1 = 21, which is known.
2. If a natural number is denoted by n, 2n is an even number and (2n + 1) an odd number.
Ex: Let n = 7; 2n = 2 × n = 2 × 7 = 14 is indeed an even number and 2n + 1 = 2 × 7 + 1 = 14 + 1 = 15 is indeed an odd number.
Pattern in geometry
1. The number of diagonals we can draw from one vertex to another of a quadrilateral is 1.
2. The number of diagonals we can draw from one vertex to another of a pentagon is 2.
3. The number of diagonals we can draw from one vertex to another of a hexagon is 3.
Thus, the number of diagonals we can draw from one vertex of a polygon of n sides is (n – 3).
Online Tuitions and Self-Study Courses for Grade 6 to 12 & JEE / NEET
